One Factor at a Time (OFAT)

And why we don't even practise what we teach...
Some "statsy" background:
OFAT (One Factor at a Time) and designed experiments are two commonly used approaches in conducting experiments in the "real world". OFAT involves testing one factor or variable at a time, while keeping all other factors constant. This method is simpler and quicker to perform compared to a designed experiment, as only one variable is being tested. OFAT is what we teach in schools and is held as the "Gold standard" of how to do an experiment (said in movie trailer man voice).
However, it has several limitations, including the inability to account for interactions between variables and the possibility of missing important effects due to confounding (something that might impact both the factors and the outcome) factors (Box & Draper, 2007; Myers, Montgomery, & Anderson-Cook, 2016). In contrast, a designed experiment involves manipulating multiple variables simultaneously to test their combined effects. In this approach, the researcher carefully chooses the levels of each factor to be tested via careful experimental design to ensure that the results are reliable and valid. This method does allow for the study of interactions and to mitigate confounding (Montgomery, 2017).
(As this will be relevant in a moment), a main effects experiment is a type of designed experiment where the researcher is interested in studying the effects of multiple factors on a single response variable. The main effect is the impact of a single factor on the response variable, and using the stats to analyse holding all other factors constant. At this point, the researcher typically uses an ANOVA (Analysis of Variance) test to determine the significance of the main effects (Box & Draper, 2007; Montgomery, 2017), often producing a "p-value". "p-values" less than 0.05 are defined as significant and the effect we are measuring is "real" and down to more than random chance.
Why is this relevant to schools / teachers?
In a word - data, or a better word "impact".
Consider running some form of "intervention" in school, where across a whole year group learners either receive the intervention or do not. We keep everything else the same for the learners. This is "OFAT" - the factor being the intervention.
Image the outcomes of the intervention are as shown in the chart:
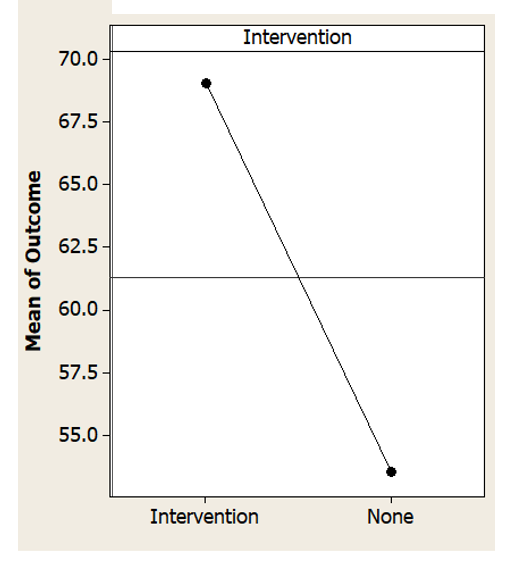
Clearly the learners receiving the intervention do far better in what is being assessed than those that don't. We might even calculate the "p-value" - in this case p=0.00, so we conclude that the intervention has a real impact on learners and commit our school to a shift in policy to adopt the intervention.
But the truth of the matter is that there are other factors changing in this setup that we haven't controlled. Notably the gender of the individual students (this is not a discussion over the gender of students, but an example of something that is "different" between learners).
If we take the same data and for the moment ignore the interventions, we get:

So, overall, regardless of intervention, "male" students out perform "female" students by the metric we have used. This insight matters as it shows something else may be going on with these learners related to teaching and learning in the school.
We can combine both these plots into what is called a "main-effects" plot - also, I have calculated the p and T values (more on that in a mo...):
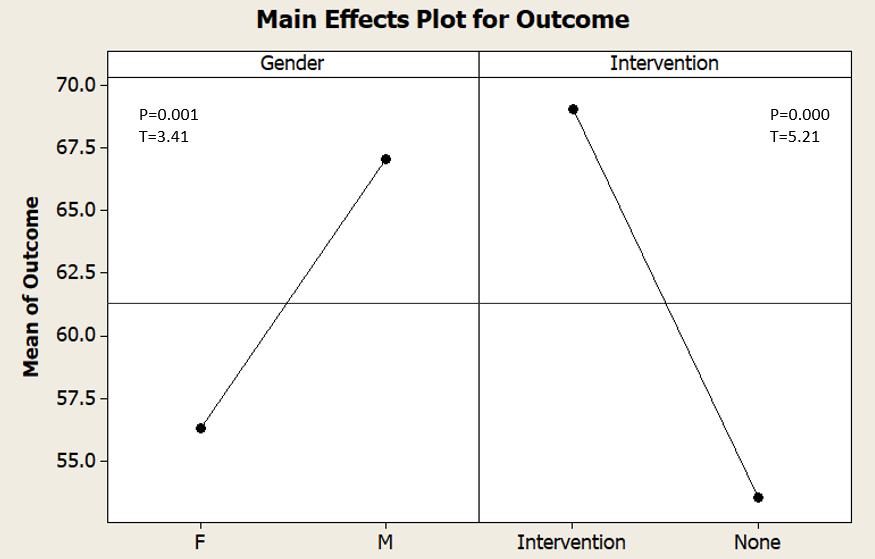
In this combined plot, you can see the effects of both "gender" and "intervention". Both have p values less than 0.05, so both are a "real" effect. The T value for Intervention is greater showing that this is a bigger impact than gender - but wait....
Let's roll back our thinking here. We undertook an intervention to "boost" performance of learners in our school. It clearly works. BUT the overall performance of "female" learners is statistically lower than the boys. Yes, the intervention works, but the data here is showing that something possibly more interesting / challenging is occurring - for reasons unknown, a whole segment of the cohort does systematically less well overall.
Regardless of the efficacy of the intervention, this main effects analysis shows that something else is going on in our school, possibly linked to culture and attitudes (why should females do less well overall? What was the teaching like? What did we try to assess?)
Why does this matter?
It matters because we teach OFAT as the only way to "do investigations". When we ourselves analyse data, we default to analysing it as OFAT even though as shown, most scenarios in education are far from OFAT.
Call to action
Consider alternatives to OFAT both when teaching "data analysis" and when looking to assess the impact in the classroom.
References:
Box, G. E., & Draper, N. R. (2007). Response surfaces, mixtures, and ridge analyses (2nd ed.). Wiley.
Montgomery, D. C. (2017). Design and analysis of experiments (9th ed.). Wiley.
Myers, R. H., Montgomery, D. C., & Anderson-Cook, C. M. (2016). Response surface methodology: process and product optimization using designed experiments (4th ed.). Wiley.
